Gdy wartość wektora prędkości w ruchu po okręgu rośnie, to rośnie też szybkość kątowa i obok przyspieszenia liniowego występuje wtedy przyspieszenie kątowe, które oznaczamy literą ε. Wyrażamy je jako stosunek przyrostu szybkości kątowej do czasu, w jakim ten przyrost nastąpił: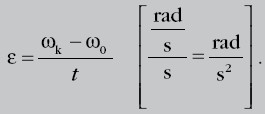
Tutaj ω0 oznacza początkową szybkość kątową (w chwili t = 0), a ωk to szybkość kątowa po czasie t (końcowa szybkość kątowa).
Warto zauważyć, że matematyczna postać tego wzoru jest identyczna ze wzorem na przyspieszenie liniowe – a, w którym zamiast szybkości kątowych występują szybkości liniowe. Podobna jest też zależność szybkości kątowej od czasu:
ωk= ω0 + ε ⋅ t
Między przyspieszeniem liniowym i kątowym podobnie jak między szybkością liniową i kątową istnieje związek:
a = ε ⋅ r
W ruchu jednostajnie przyspieszonym po okręgu mamy:
a=const i ε = const.
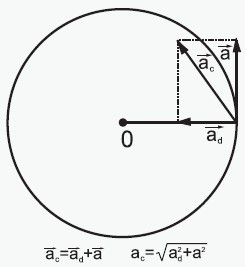
W ruchu przyspieszonym po okręgu występują następujące przyspieszenia:
- przyspieszenie dośrodkowe – ad, związane wyłącznie ze zmianą kierunku i zwrotu wektora prędkości liniowej,
- przyspieszenie liniowe – a, związane ze zmianą wartości wektora prędkości liniowej,
- przyspieszenie kątowe – ε, które jest spowodowane przyspieszeniem a.